07-31-2021, 10:25 AM
Now I show how to use the third plugin Parametric curve (read function from file). The details are explained in doc.pdf, so if you are interested, please read it. I show here two examples. The file doc.py contains two other examples.
I don't do much explanations here. For more details and better explanations, please look at doc.pfd.
The GUI is almost the same as for the other two plugins, but instead of functions x(t), y(t), or r(t), it asks for a file.
Example 1: The cochleoid
To follow this example, make a file with the following contents. Note that it must be valid Python code, so care must be taken of indentations for example.
Save the file as somefile.py to somewhere where it is easily found (desktop perhaps). Open the GUI of the plugin, and there choose the file somefile.py. Press OK. If everything is ok you get the following curve, called the cochleoid:
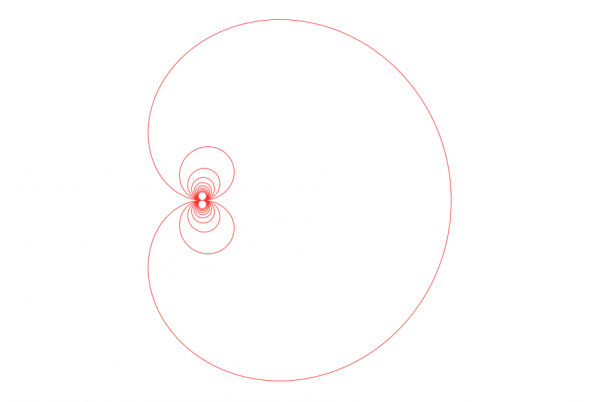
Explanation: The file is valid Python code. There "def function(t):..." implements the function for the cochleoid curve. The "interval = ..." defines which part of the curve will be drawn.
In the definition of the function, I mention a couple of points for those interested: The function must return a complex number (the plane is viewed as the complex number plane). The defining equation for the cochleoid in polar form is r=sin(t)/t. In the code the factor "*cexp(1j*t)" converts it to proper complex-valued function. The exception ZeroDivisionError occurs when t=0, and there the limit value sin(t)/t -> 1 is used.
Example 2: Experimenting
The formula for the cochleoid in polar form is r = sin(t)/t where t is the argument angle (or polar angle = angle from the positive x axis).
Quite by chance I happened to see yesterday a similar formula r = sin(n*t)/sin(t) while surfing in search of something else. Since I now have this system which makes it easy to experiment with such formulas, I had to try this one. I wrote the following piece of code in a file:
Here n is a parameter, a positive integer. To change it I have to edit it in the file. When we vary n, the curves follow two patterns. With odd n the curve is symmetric both in x and y directions, but with even n the symmetry in x direction is lost. A typical odd case is given by n=7:
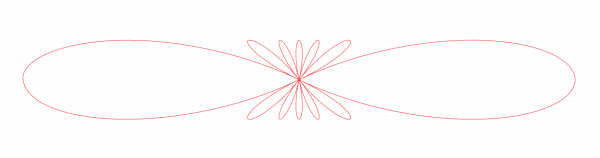
The larger n, the larger the number of petals. This looks nice, don't you think? I can imagine that from these one could build a pretty ornament. And it is a path, so the user is free to choose any stroking.
If you have any questions, just ask. Notice that this plugin enables you to write complicated functions since you have free hands to do any Python coding. But it may happen that the plugin cannot handle all inputs. It is written by me, after all, and I am not much of a coder, and since I know the inner structures of the plugin with all those ad hoc solutions and fine-tunings, I know that much can fail. If you run into troubles with the plugin, I would be interested to hear about it.
I don't do much explanations here. For more details and better explanations, please look at doc.pfd.
The GUI is almost the same as for the other two plugins, but instead of functions x(t), y(t), or r(t), it asks for a file.
Example 1: The cochleoid
To follow this example, make a file with the following contents. Note that it must be valid Python code, so care must be taken of indentations for example.
Code:
def function(t): # cochleoid
from cmath import exp as cexp
try:
r = sin(t)/t
except ZeroDivisionError:
r = 1
return r*cexp(1j*t)
curve_name = 'cochleoid'
interval = [-10*pi, 10*pi]
closed = FalseSave the file as somefile.py to somewhere where it is easily found (desktop perhaps). Open the GUI of the plugin, and there choose the file somefile.py. Press OK. If everything is ok you get the following curve, called the cochleoid:
Explanation: The file is valid Python code. There "def function(t):..." implements the function for the cochleoid curve. The "interval = ..." defines which part of the curve will be drawn.
In the definition of the function, I mention a couple of points for those interested: The function must return a complex number (the plane is viewed as the complex number plane). The defining equation for the cochleoid in polar form is r=sin(t)/t. In the code the factor "*cexp(1j*t)" converts it to proper complex-valued function. The exception ZeroDivisionError occurs when t=0, and there the limit value sin(t)/t -> 1 is used.
Example 2: Experimenting
The formula for the cochleoid in polar form is r = sin(t)/t where t is the argument angle (or polar angle = angle from the positive x axis).
Quite by chance I happened to see yesterday a similar formula r = sin(n*t)/sin(t) while surfing in search of something else. Since I now have this system which makes it easy to experiment with such formulas, I had to try this one. I wrote the following piece of code in a file:
Code:
n = 7 # integer > 0
def function(t):
from cmath import exp as cexp
try:
r = sin(n*t)/sin(t)
except ZeroDivisionError:
r = n*cos(n*t)/cos(t) # limit by l'Hospital
return r*cexp(1j*t)
curve_name = 'experiment n='+str(n)
if n%2 == 0:
interval = [0,pi]
else:
interval = [0,2*pi]
closed = TrueHere n is a parameter, a positive integer. To change it I have to edit it in the file. When we vary n, the curves follow two patterns. With odd n the curve is symmetric both in x and y directions, but with even n the symmetry in x direction is lost. A typical odd case is given by n=7:
The larger n, the larger the number of petals. This looks nice, don't you think? I can imagine that from these one could build a pretty ornament. And it is a path, so the user is free to choose any stroking.
If you have any questions, just ask. Notice that this plugin enables you to write complicated functions since you have free hands to do any Python coding. But it may happen that the plugin cannot handle all inputs. It is written by me, after all, and I am not much of a coder, and since I know the inner structures of the plugin with all those ad hoc solutions and fine-tunings, I know that much can fail. If you run into troubles with the plugin, I would be interested to hear about it.



