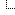03-19-2020, 07:48 PM
In this post I show some examples of what the plugin Parametric curves can do when the inputs are passed to it in a file. This is much more powerful than merely typing inputs in the GUI. Indeed, to take full benefit of the plugin, this is the way to go.
Below are five examples. They are drawn by the plugin taking inputs from a file. The five input files are found in the folder example_files in the .zip file. And there are many more. If you get interested, you can try all the example files in the folder one by one to see what they draw. You can also read the files (Python code) and perhaps try to make changes. And when looking at the results, please take notice of the main feature of the plugin: the control points on the paths will be indeed sparse even when the approximation is rather good!
1. The curve astroid is defined by f(t) = (cos(t)**3, sin(t)**3). It has four cusps. To get the cusps right they can be inputted as custom parameter values as is done here, but this plugin does find them rather well even without any help.

2. The GUI allows inputting functions in the form f(t)=(x(t),y(t)). But when the inputs are taken from a file, the user has available all resources of programming. As an example, the following figure is a result of playing with the equation of astroid.
To define the curve, the input file defines the parametric function as follows:
Just think what a job it would to type this function in the GUI as x(t) and y(t)! And in the GUI there is no way to save what one typed!
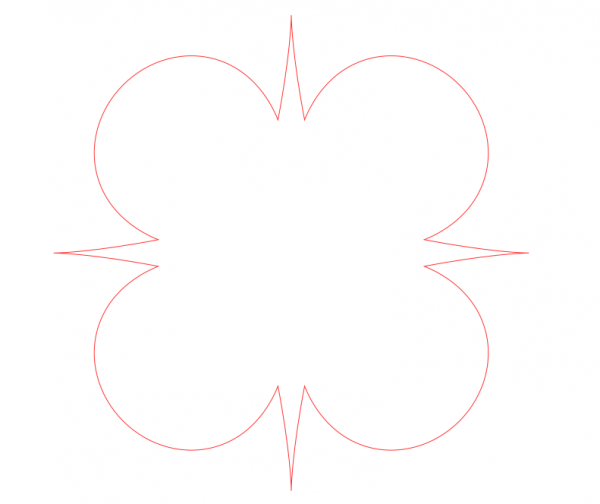
3. The plugin is designed to draw several parametric curves in the same picture, another central feature. (That is not possible in the GUI, and not at all with the simple plugin.) Here is an example where there are two circles and one ellipse. In addition there are some line segments; that is another feature of the plugin.
4. A rose or rhodonea has the polar equation r = cos(kt)+c; for the formula and other info see
https://en.wikipedia.org/wiki/Rose_(mathematics)
One of the example files is an implementation of the case k = a/b where a,b are integers. The case a,b,c = 5,6,0 looks as follows (edit the file if you want to try others):

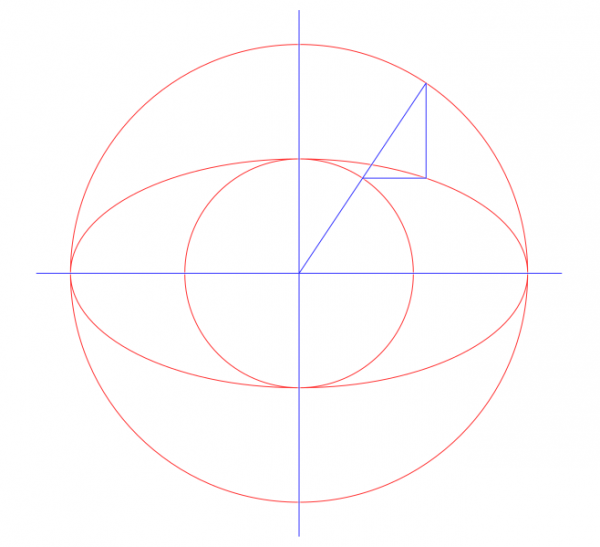
5. The final example here is the graph of the normal distribution. The curve is the Bezier approximation. In the same picture the little stars show where the exact curve would run. That is another feature, meant to enable the user to see quite visually how good or bad the approximation is. We see that in this example at least the approximation is satisfactory.
For preliminaries on writing such input files, please see the documentation file doc.pdf. Another source of help is the example files. And the folder example_files has a subfolder called templates which contains three template files. They are meant to easify writing input files.
And of course, you can come here and ask any questions. If you have some figure you would like to create, just ask and perhaps I can help.
Below are five examples. They are drawn by the plugin taking inputs from a file. The five input files are found in the folder example_files in the .zip file. And there are many more. If you get interested, you can try all the example files in the folder one by one to see what they draw. You can also read the files (Python code) and perhaps try to make changes. And when looking at the results, please take notice of the main feature of the plugin: the control points on the paths will be indeed sparse even when the approximation is rather good!
1. The curve astroid is defined by f(t) = (cos(t)**3, sin(t)**3). It has four cusps. To get the cusps right they can be inputted as custom parameter values as is done here, but this plugin does find them rather well even without any help.
2. The GUI allows inputting functions in the form f(t)=(x(t),y(t)). But when the inputs are taken from a file, the user has available all resources of programming. As an example, the following figure is a result of playing with the equation of astroid.
To define the curve, the input file defines the parametric function as follows:
Code:
def astroid_play(t):
R = 0.75 # Choose a number between 0.5 and 1
x,y = cos(t)**3, sin(t)**3 # Astroid
r = sqrt(x**2 + y**2) # Radius
r1 = R + abs(r-R) # To reflect points with r<R in circle r=R
r1 = r1**2 # To get stronger effect
return [(r1/r)*x, (r1/r)*y]Just think what a job it would to type this function in the GUI as x(t) and y(t)! And in the GUI there is no way to save what one typed!
3. The plugin is designed to draw several parametric curves in the same picture, another central feature. (That is not possible in the GUI, and not at all with the simple plugin.) Here is an example where there are two circles and one ellipse. In addition there are some line segments; that is another feature of the plugin.
4. A rose or rhodonea has the polar equation r = cos(kt)+c; for the formula and other info see
https://en.wikipedia.org/wiki/Rose_(mathematics)
One of the example files is an implementation of the case k = a/b where a,b are integers. The case a,b,c = 5,6,0 looks as follows (edit the file if you want to try others):
5. The final example here is the graph of the normal distribution. The curve is the Bezier approximation. In the same picture the little stars show where the exact curve would run. That is another feature, meant to enable the user to see quite visually how good or bad the approximation is. We see that in this example at least the approximation is satisfactory.
For preliminaries on writing such input files, please see the documentation file doc.pdf. Another source of help is the example files. And the folder example_files has a subfolder called templates which contains three template files. They are meant to easify writing input files.
And of course, you can come here and ask any questions. If you have some figure you would like to create, just ask and perhaps I can help.