06-08-2020, 11:08 AM
I have updated the plugins to version 0.12. The link is in post #1. The .ZIP file contains everything. What is new is the Möbius transformation. Actually there are four plugins to perform a Möbius mapping. The main one will be found in Gimp's menu (after right-clicking the path you want to transform) at
Tools > Transformations > Moebius map
and then there are three more at
Tools > Transformations > Moebius map with control of poles > ...
In this post I talk about the first one. Later I shall make a separate post about the other three.
I stress the fact that in some cases the plugin may be so slow that the user wants to interrupt it. Therefore, one had better know how to stop it without stopping Gimp (in Windows 10 it is the Task Manager), and in any case it is good to save one's work before trying the plugin. In practice, it may be wise to experiment first using the simple algorithm (see below), and only when one has found what one likes, to realize it with the good but slow algorithm.
For mathematical background on the Möbius map, you can look at
https://en.wikipedia.org/wiki/M%C3%B6biu...sformation
I list here only the most crucial features of Möbius maps:
In the following picture on the left I show what the Base and the Target might look like. They are three-anchor paths; only the anchors are taken into account, and all curviness is ignored.
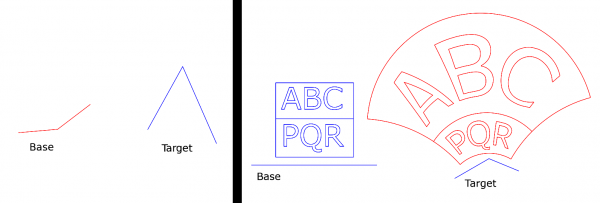
On the right you see what the plugin does in practice. Here I used a straight Base and a slightly bending Target. The path to be transformed (blue) is the letters ABCPQR "framed" by straight edges. The result is shown in red in the same picture. Note that the straight edges are mapped onto circular arcs.
In the next picture below, on the left is a figure consisting of three astroids (blue, drawn by means of my Parametric curves plugin) and the transformed path (red). Again I used a straight Base.
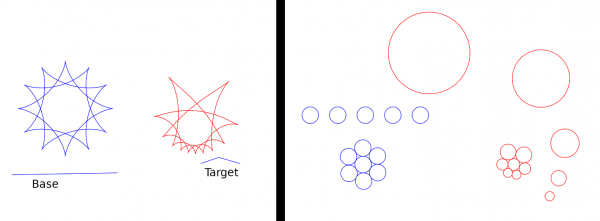
On the right I want to show that circles are indeed sent to circles. The Base (straight) and the Target are there but set to unvisible in this picture. The original path is the blue set of 12 circles, and the transformed path is the red circles. You see that the circles are indeed sent to circles. Note also that the five blue circles in a straight row are sent to circles of increasing sizes which (just believe it!) have their centers on another circle.
(By the way, to create the original circles I used the Parametric curves plugin and Gimp's copying and moving tools.)
Just as in post #6, the plugin offers the choice of the algorithm. Input 0 gives the good but slooow algorithm. Inputs 1,2,... invoke a simple algorithm, quick but inaccurate. Higher number means better accuracy but with the cost of increasing number of control points. The behaviour differs now from the previous version in that the number of control points grows exponentially with the input number. For that reason the plugin forces the input number to <=8. I expect that in practice 2..5 will suffice, depending on the case.
If you have any problems with the plugins, please let me know. It has become so complicated that it seems that almost every time when I think it is ready to be published, and I am just making example pictures, the plugin fails somehow. Then I just have go back to the code to find out what I have overlooked this time. Every case where the plugin fails is invaluable for finding bugs, so please report.
Tools > Transformations > Moebius map
and then there are three more at
Tools > Transformations > Moebius map with control of poles > ...
In this post I talk about the first one. Later I shall make a separate post about the other three.
I stress the fact that in some cases the plugin may be so slow that the user wants to interrupt it. Therefore, one had better know how to stop it without stopping Gimp (in Windows 10 it is the Task Manager), and in any case it is good to save one's work before trying the plugin. In practice, it may be wise to experiment first using the simple algorithm (see below), and only when one has found what one likes, to realize it with the good but slow algorithm.
For mathematical background on the Möbius map, you can look at
https://en.wikipedia.org/wiki/M%C3%B6biu...sformation
I list here only the most crucial features of Möbius maps:
- A Möbius map is actually a transformation on the extended plane (=plane + a point at infinity). For simplicity, I side-step now infinities altogether (postponed to the next post).
- Given any triple A,B,C of distinct points and another triple X,Y,Z of distinct points, there is precisely one Möbius map sending A->X, B->Y, and C->Z.
- A Möbius map is conformal: all angles are preserved.
- Circular arcs are sent to circular arcs.
- But here "circles" include straight lines, since a straight line is viewed as an infinite circle. (Ok, here the infinity comes in after all!) Therefore, the image of any straight line segment will be a circular arc (or in rare cases another line segment).
- No Shaper is used.
- The Base and the Target are paths with three anchors each. These will give the points A,B,C and X,Y,Z.
- Line segments are normally sent to circular arcs (rather than to copies of a Shaper).
- The plugin offers an easy way to use the 3 anchors of the Base in any of their 6 permutations.
- And then there is the infinity which may cause surprises. But about that in another post.
In the following picture on the left I show what the Base and the Target might look like. They are three-anchor paths; only the anchors are taken into account, and all curviness is ignored.
On the right you see what the plugin does in practice. Here I used a straight Base and a slightly bending Target. The path to be transformed (blue) is the letters ABCPQR "framed" by straight edges. The result is shown in red in the same picture. Note that the straight edges are mapped onto circular arcs.
In the next picture below, on the left is a figure consisting of three astroids (blue, drawn by means of my Parametric curves plugin) and the transformed path (red). Again I used a straight Base.
On the right I want to show that circles are indeed sent to circles. The Base (straight) and the Target are there but set to unvisible in this picture. The original path is the blue set of 12 circles, and the transformed path is the red circles. You see that the circles are indeed sent to circles. Note also that the five blue circles in a straight row are sent to circles of increasing sizes which (just believe it!) have their centers on another circle.
(By the way, to create the original circles I used the Parametric curves plugin and Gimp's copying and moving tools.)
Just as in post #6, the plugin offers the choice of the algorithm. Input 0 gives the good but slooow algorithm. Inputs 1,2,... invoke a simple algorithm, quick but inaccurate. Higher number means better accuracy but with the cost of increasing number of control points. The behaviour differs now from the previous version in that the number of control points grows exponentially with the input number. For that reason the plugin forces the input number to <=8. I expect that in practice 2..5 will suffice, depending on the case.
If you have any problems with the plugins, please let me know. It has become so complicated that it seems that almost every time when I think it is ready to be published, and I am just making example pictures, the plugin fails somehow. Then I just have go back to the code to find out what I have overlooked this time. Every case where the plugin fails is invaluable for finding bugs, so please report.



