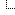Posts: 1,063
Threads: 88
Joined: Aug 2018
Reputation:
83
Gimp version:
Operating system(s): Windows Vista or 7, 8, 10 (64-bit)
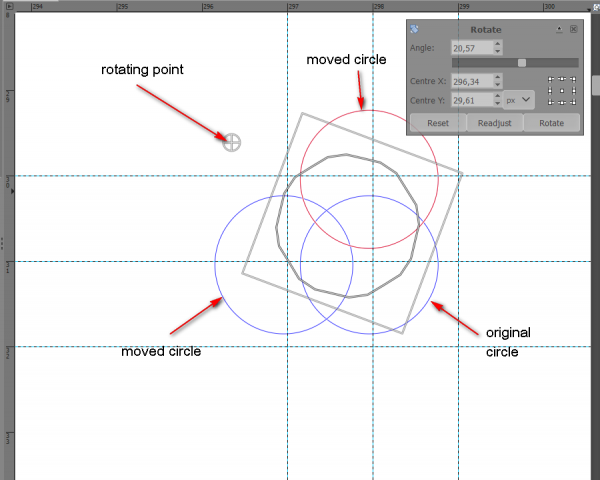
What I could see is that after rotating the circles their diameters were changed.
The original circle is 200x200.
Made two copies and rotated both at an angle of 20.57, the dimensions of both were changed to 202x201.
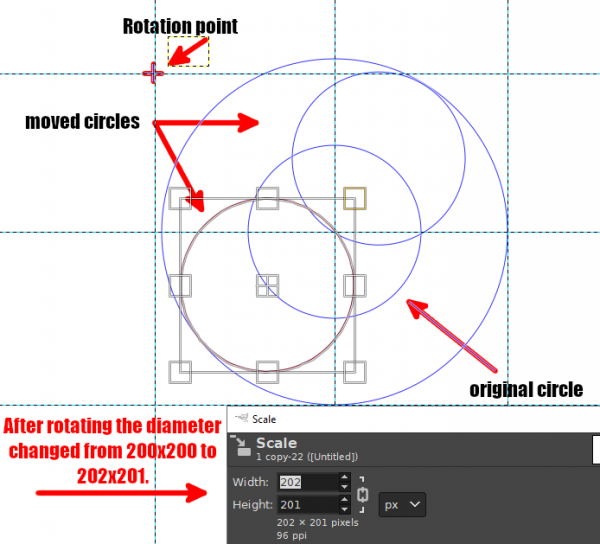
By centering on the screen, the enlarged circles had a different center.
.....
Samj Portable - Gimp 2.10.28 - Win-10 /64.
Posts: 1,398
Threads: 216
Joined: Sep 2018
Reputation:
129
Gimp version:
Operating system(s): Windows 11
@Krikor, I also noticed that. That's probably because if rotated the circle is no more on the crossing line of pixels. I think that the values from the coordinates on the new position are rounded to an even value and this is reflected on the circle. I could be wrong.
Posts: 1,063
Threads: 88
Joined: Aug 2018
Reputation:
83
Gimp version:
Operating system(s): Windows Vista or 7, 8, 10 (64-bit)
@denzjos,
I thought the problem could originate if the center of rotation was not an integer (non-decimal) point (x,y).
But I did some tests, creating rotation points in integer coordinates and even then the problem was repeated.
In the image below, the original circle
(100x100) after being rotated using the
Rotate Tool 
, was changed to
101x101.
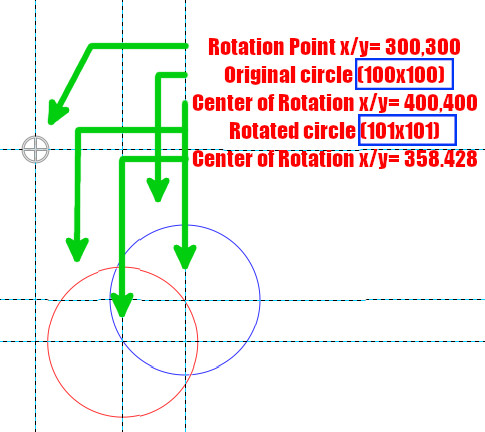
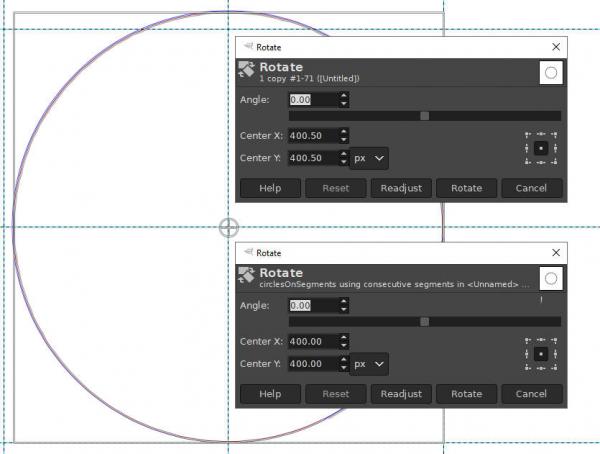
I did another test, this time using the plugin (
Duplicate and Rotate a Path...), and as the image below illustrates, there was also a change in the dimensions of the circles after rotation in 100% of the created and rotated copies.
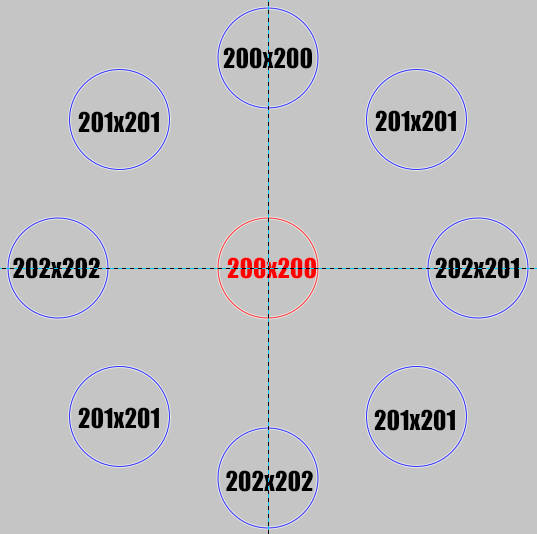
.....
Samj Portable - Gimp 2.10.28 - Win-10 /64.
Posts: 6,949
Threads: 297
Joined: Oct 2016
Reputation:
605
Gimp version:
Operating system(s): Linux
A path circle isn't a perfect circle, it is an approximation.Since it is not perfect, the diameter isn't constant and under some angles it can be bigger or smaller than the ideal diameter, so you can indeed see an increase of diameter when you rotate it. In paths constructed with ofn-path-to-shape, points at 45° intervals (starting from the segment that was used to construct the circle) are exactly on the circle.