03-18-2022, 05:24 PM
I made a plugin which, given a path as input, creates a smooth path through its anchors. You may remember that I already made one such simple plugin:
https://www.gimp-forum.net/Thread-Smooth...ple-plugin
but now I have a better algorithm. Instead of that simple plugin, this new plugin (named "G2-continuity") should be compared to the old smooth-path.exe:
https://www.gimp-forum.net/Thread-Rich-I...0#pid28230
That old plugin makes C2-continuous paths. The new plugin does that too, but it makes also more general G2-continuous paths.
To get the plugin, go to
http://kmarkku.arkku.net/Path_modify_fil...aster.html
scroll to the bottom, and click the right download button ("G2-continuity"). You get a zip file. Unzip it and place the one file it contains (G2_continuity.py) in your user's plug-ins folder. Then (re)start Gimp. To use the plugin: in the Paths tab, right-click a path and follow the links Tools > Modify path > G2-continuity.
A picture using the default values:
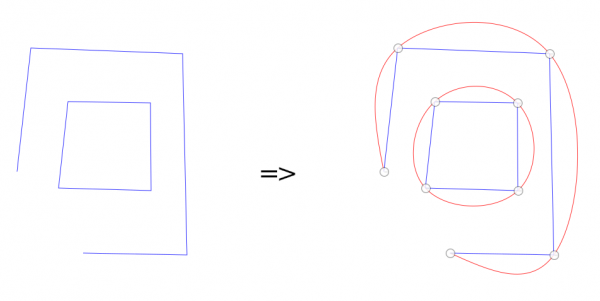
The blue path is the input path, and the red path is the path made by the plugin. So, this is another method to draw a smooth path through some given points.
We had some discussion of C2-continuity with Ofnuts in:
https://www.gimp-forum.net/Thread-Rich-I...6#pid28246
C2-continuity is about derivatives of the parametric representation of the curve. So, it is very mathematical. We use now another concept, G2-continuity (the 'G' coming from "geometric"), which is more directly connected with the visual appearance of the curve and independent of the parametric representation. It means that the curve is smooth and has continuous curvature. For paths G2-continuity means:

C2-continuity makes at the short edge an unnecessarily prominent arc. I would like better a smaller arc, see the picture. The reason why C2-continuity gives such a strong arc is the continuity of the first derivative: it forces the handles at an anchor to be of equal length (symmetric). But I think it would be better if the handle on the longer edge would be longer and the handle on the shorter edge would be shorter, like this:

So I think that the edge lengths should be taken into account when making the handles. But then C2-continuity is no longer possible, not even C1-continuity. But G2-continuity is possible. And I think that it is this condition which really counts visually. Continuous curvature means that the curve is very smooth.
So I took the theory in
https://www.stkent.com/2015/07/03/buildi...urves.html
and modified it suitably to take into account edge lengths, producing G2-continuous paths (and since that can be done in infinitely many ways I had to do some ad hoc choices). I also did the case of closed strokes and added some embellishments. No need to go into further details. It was rather pleasing work to do.
Be kind enough to tell me if you find cases where the plugin works wrong.
There are two tuning parameters. I try to explain what they do though you may do wisest if you just go experimenting.
The first tuning parameter: Let us consider a straight-edge path. The tuning parameter adjusts how strongly the different lengths of the edges are taken into account; see the above pictures. Let us call the parameter K. If K=0 the lengths are not taken into account at all, just like in C2-continuity. I put K=1 as the default since I think it gives nice results.
The second tuning parameter determines how tightly the curve will bend at anchors. C2-continuity allows no such adjustings, but with G2-continuity this can be done.
The way I implemented the two tuning parameters is very ad hoc and could be done in infinitely many different ways, still getting G2-continuity. I could easily make the plugin to have 10 tuning parameters, say, but who would want it? I think 2 parameters is optimal.
There is also an option on how the end parts of open strokes are treated. This is useful only if the original path has some curvature and you want to preserve the tangent directions at open stroke ends:
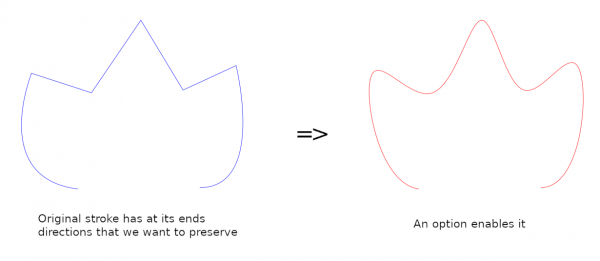
This option arose from a mathematical reason. If you look at the text by Stuart Kent you see that if an open stroke has n+1 anchors (knots) then the requirement of C2-continuity gives us a big group of equations with 2n unknowns and 2n-2 equations. So, to solve the group we need two additional equations. They can be chosen freely. For those two, Kent takes what he calls "natural boundary conditions": f''=0 at each end of the stroke. It occurred to me that we could use some other boundary conditions. I chose to preserve tangent directions at the ends; this seemed neat, easy to grasp, and sometimes useful.
There are two options about using a selection. They should be clear enough, so I say nothing about those here.
https://www.gimp-forum.net/Thread-Smooth...ple-plugin
but now I have a better algorithm. Instead of that simple plugin, this new plugin (named "G2-continuity") should be compared to the old smooth-path.exe:
https://www.gimp-forum.net/Thread-Rich-I...0#pid28230
That old plugin makes C2-continuous paths. The new plugin does that too, but it makes also more general G2-continuous paths.
To get the plugin, go to
http://kmarkku.arkku.net/Path_modify_fil...aster.html
scroll to the bottom, and click the right download button ("G2-continuity"). You get a zip file. Unzip it and place the one file it contains (G2_continuity.py) in your user's plug-ins folder. Then (re)start Gimp. To use the plugin: in the Paths tab, right-click a path and follow the links Tools > Modify path > G2-continuity.
A picture using the default values:
The blue path is the input path, and the red path is the path made by the plugin. So, this is another method to draw a smooth path through some given points.
We had some discussion of C2-continuity with Ofnuts in:
https://www.gimp-forum.net/Thread-Rich-I...6#pid28246
C2-continuity is about derivatives of the parametric representation of the curve. So, it is very mathematical. We use now another concept, G2-continuity (the 'G' coming from "geometric"), which is more directly connected with the visual appearance of the curve and independent of the parametric representation. It means that the curve is smooth and has continuous curvature. For paths G2-continuity means:
- At every anchor the two tangents are parallel (the same). But the handles need not be symmetric, that is, of equal length.
- At every anchor the two curvatures are equal. This means that the two circles of curvature at the anchor are the same.
C2-continuity makes at the short edge an unnecessarily prominent arc. I would like better a smaller arc, see the picture. The reason why C2-continuity gives such a strong arc is the continuity of the first derivative: it forces the handles at an anchor to be of equal length (symmetric). But I think it would be better if the handle on the longer edge would be longer and the handle on the shorter edge would be shorter, like this:
So I think that the edge lengths should be taken into account when making the handles. But then C2-continuity is no longer possible, not even C1-continuity. But G2-continuity is possible. And I think that it is this condition which really counts visually. Continuous curvature means that the curve is very smooth.
So I took the theory in
https://www.stkent.com/2015/07/03/buildi...urves.html
and modified it suitably to take into account edge lengths, producing G2-continuous paths (and since that can be done in infinitely many ways I had to do some ad hoc choices). I also did the case of closed strokes and added some embellishments. No need to go into further details. It was rather pleasing work to do.
Be kind enough to tell me if you find cases where the plugin works wrong.
There are two tuning parameters. I try to explain what they do though you may do wisest if you just go experimenting.
The first tuning parameter: Let us consider a straight-edge path. The tuning parameter adjusts how strongly the different lengths of the edges are taken into account; see the above pictures. Let us call the parameter K. If K=0 the lengths are not taken into account at all, just like in C2-continuity. I put K=1 as the default since I think it gives nice results.
The second tuning parameter determines how tightly the curve will bend at anchors. C2-continuity allows no such adjustings, but with G2-continuity this can be done.
The way I implemented the two tuning parameters is very ad hoc and could be done in infinitely many different ways, still getting G2-continuity. I could easily make the plugin to have 10 tuning parameters, say, but who would want it? I think 2 parameters is optimal.
There is also an option on how the end parts of open strokes are treated. This is useful only if the original path has some curvature and you want to preserve the tangent directions at open stroke ends:
This option arose from a mathematical reason. If you look at the text by Stuart Kent you see that if an open stroke has n+1 anchors (knots) then the requirement of C2-continuity gives us a big group of equations with 2n unknowns and 2n-2 equations. So, to solve the group we need two additional equations. They can be chosen freely. For those two, Kent takes what he calls "natural boundary conditions": f''=0 at each end of the stroke. It occurred to me that we could use some other boundary conditions. I chose to preserve tangent directions at the ends; this seemed neat, easy to grasp, and sometimes useful.
There are two options about using a selection. They should be clear enough, so I say nothing about those here.





