07-12-2020, 12:50 PM
(This post was last modified: 07-12-2020, 01:59 PM by Ottia Tuota.)
I made another path transformation plugin. It is based on an idea of my own. But I cannot believe that no predecessors would exist. The idea is so simple.
The link to download the plugin (and all the previous ones) is in post #1. It is a .zip file but contains one big file only. The version is now 0.15.
Better to start with a picture:
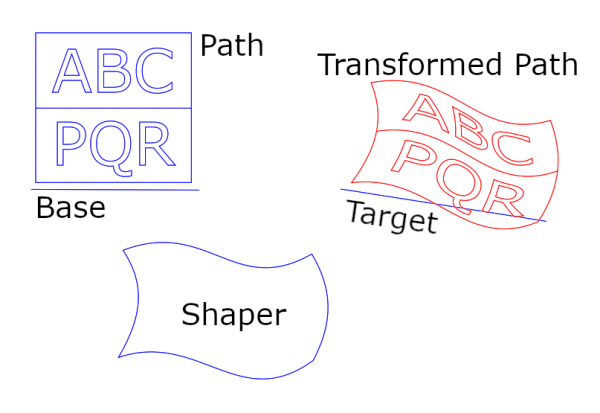
The input paths in this picture are:
In the plugin I assumed that the Shaper is a simple curvy quadrilateral covering roughly a rectangular region. Anything else may work ok, or it may give weird results. I also assumed that the edges of the Shaper run roughly: horizontal-vertical-horizontal-vertical, but that is not so necessary to get good results.
The plugin is somewhat similar to the one in post #3. Main differences are:
 transformation_by_16_bezier.pdf (Size: 247.04 KB / Downloads: 536)
transformation_by_16_bezier.pdf (Size: 247.04 KB / Downloads: 536)
My plugin transforms paths, but from the formulas somebody more skilled could write a tool for transforming images.
I admit that the results are not always so neat as in the few pictures in this post. The Bernstein polynomials are of degree 3, after all, and they tend to grow fast. So the outcomes are not easy to control, and one has just to go experimenting and trying to learn to use the plugin. I haven't much done that myself since this is quite new and I have a lot of other things to do. If the plugin goes too wild, one can curb the Shaper by the input 'strength'. Another good rule is to place the Base quite close to the Path.
There is another way to use the the plugin: Base and Target may have 4 anchors. This allows the user to have some particular four points mapped onto some other particular four points. A picture:
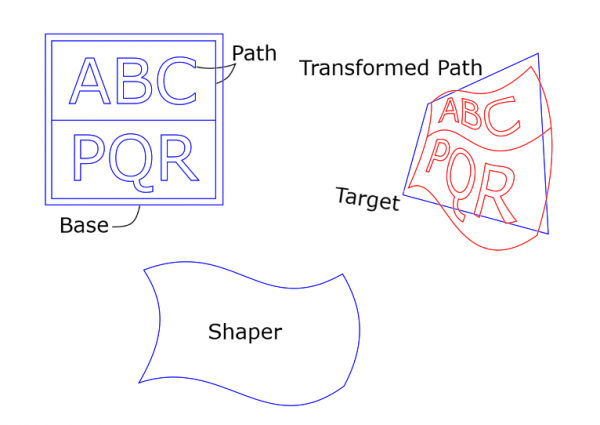
The Path is the text ABCPQR together with the frame. The Base is the slightly bigger square. The Target is the skew quadrilateral. The corner points of the Base are mapped onto the corner points of the Target. The Transformed Path (red) is distorted accordingly. (If I had put the Base exactly at the frame of the Path, the corners of the frame would have been mapped exactly at the corners of the Target. Now there is a little discrepancy.)
A word of warning: When one uses Base and Target with four anchors, the plugin may fail with message like "Hit an infinity". Namely, here the plugin uses projective transformations (I think it is almost the same as Gimp's Perspective transform), and infinities occur quite naturally. So, such failure is not necessarily a sign of a fault with the plugin. If that happens, make changes in the input paths and try again.
Now I explain the other inputs in the GUI of the plugin.
The three 'Permute' inputs you need not touch at all. If the input paths are reasonable, the results should be reasonable. But you can experiment.
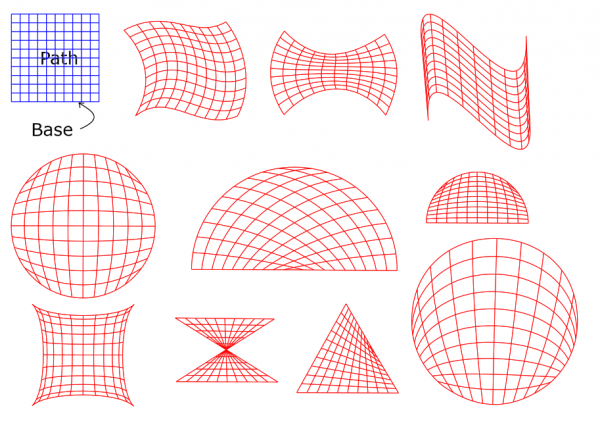
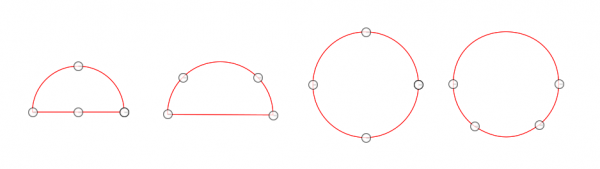
Note in particular the two half circles: the outline is the same but the curved grids inside are different. The secret is that in each the Shaper was a half circle but the anchors on that half circle were placed differently. In other words, the subdivisions of the Shapers into four arcs were different. The same is true for the two circlular cases. And having said that much, I also have to show how the anchors in the Shapers were situated (the handles are not shown):
I hope you enjoy. Any feedback or questions are welcome!
Edit: Deleted one remark. Wrong idea.
The link to download the plugin (and all the previous ones) is in post #1. It is a .zip file but contains one big file only. The version is now 0.15.
Better to start with a picture:
The input paths in this picture are:
- The Path to be transformed (the letters ABCPQR with the frame)
- The Base, a path with 2 anchors
- The Target, a path with 2 anchors
- The Shaper, a curvy quadrilateral consisting of four Bezier arcs (closed, four anchors)
In the plugin I assumed that the Shaper is a simple curvy quadrilateral covering roughly a rectangular region. Anything else may work ok, or it may give weird results. I also assumed that the edges of the Shaper run roughly: horizontal-vertical-horizontal-vertical, but that is not so necessary to get good results.
The plugin is somewhat similar to the one in post #3. Main differences are:
- This transformation is not conformal.
- The Shaper is made of 4 Bezier arcs (rather than just 1).
- The plugin also allows Base and Target with 4 anchors.
 transformation_by_16_bezier.pdf (Size: 247.04 KB / Downloads: 536)
transformation_by_16_bezier.pdf (Size: 247.04 KB / Downloads: 536)
My plugin transforms paths, but from the formulas somebody more skilled could write a tool for transforming images.
I admit that the results are not always so neat as in the few pictures in this post. The Bernstein polynomials are of degree 3, after all, and they tend to grow fast. So the outcomes are not easy to control, and one has just to go experimenting and trying to learn to use the plugin. I haven't much done that myself since this is quite new and I have a lot of other things to do. If the plugin goes too wild, one can curb the Shaper by the input 'strength'. Another good rule is to place the Base quite close to the Path.
There is another way to use the the plugin: Base and Target may have 4 anchors. This allows the user to have some particular four points mapped onto some other particular four points. A picture:
The Path is the text ABCPQR together with the frame. The Base is the slightly bigger square. The Target is the skew quadrilateral. The corner points of the Base are mapped onto the corner points of the Target. The Transformed Path (red) is distorted accordingly. (If I had put the Base exactly at the frame of the Path, the corners of the frame would have been mapped exactly at the corners of the Target. Now there is a little discrepancy.)
A word of warning: When one uses Base and Target with four anchors, the plugin may fail with message like "Hit an infinity". Namely, here the plugin uses projective transformations (I think it is almost the same as Gimp's Perspective transform), and infinities occur quite naturally. So, such failure is not necessarily a sign of a fault with the plugin. If that happens, make changes in the input paths and try again.
Now I explain the other inputs in the GUI of the plugin.
The three 'Permute' inputs you need not touch at all. If the input paths are reasonable, the results should be reasonable. But you can experiment.
- Permute the Base anchors: If the result is not what you expected, you can try to use the Base with its anchors permuted with cyclic rotation and/or reversed. When the Base has 4 anchors, the meaning of the input number is: 0..3 are rotations (0 does nothing) and 4..7 are rotations followed by reversal. When the Base has 2 anchors, there are two alternatives: 0 (or any even number) does nothing, and 1 (or any odd number) causes reversal.
- Permute the Target anchors: This is the same operation for the Target.
- Permute the Shaper anchors: This is the same operation for the Shaper (with always 4 anchors).
- Linearize any straight edges in Shaper: If the Shaper contains a straight edge, its handles may be of zero length, or they may be something else, without any visual difference. But different handle lengths result in different transformations. When the input 'Linearize' is Yes, the plugin internally sets the handles at points 1/3 and 2/3 of the straight edge. This tames a little the transformation which might otherwise be more distorting than desired. (Mathematically: the Bezier function coming from such an edge is made a linear function.)
- Adjust the form of shaping: Experiment.
- Strength of Shaper: Adjust the effect of the curviness of the Shaper. If strength=1, the Shaper is used as is. If strength=0, the Shaper is used with its edges straightened out. If 0<strength<1, the effect is something between.
- Choose algorithm (integer 0..8): The plugin is very slow. By choosing a number >0 the user can make the plugin to use a worse but fast simple algorithm. The idea is to do experimenting with such fast algorithm, and when something good is found, finally draw it with the good but slow algorithm.
Note in particular the two half circles: the outline is the same but the curved grids inside are different. The secret is that in each the Shaper was a half circle but the anchors on that half circle were placed differently. In other words, the subdivisions of the Shapers into four arcs were different. The same is true for the two circlular cases. And having said that much, I also have to show how the anchors in the Shapers were situated (the handles are not shown):
I hope you enjoy. Any feedback or questions are welcome!
Edit: Deleted one remark. Wrong idea.



